Abstract
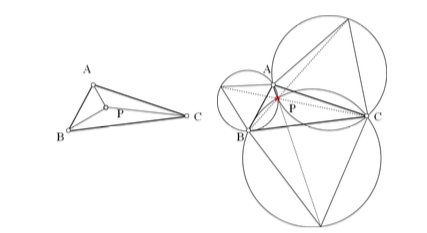
This paper explores a geometric approach to finding optimal routes for commercial formation flight. A weighted extension of the classical Fermat point problem is used to develop an analytic solution to finding optimal routes, thereby reducing the complexity of the problem and enabling a quick evaluation. We then construct a method to decouple origin and destination nodes creating a vertex from which the route projects, along with loci of possible points of formation. This implementation enables us to take lists of routes and efficiently decompose them to find the optimal locations for flights to meet, fly in formation and then break away and continue on their solo paths. We look at a case study of creating formations from 210 transatlantic flights for a fleet size of up to 2, resulting in overall global approximate total fuel savings of 8.6%. Furthermore we explore heuristic methods to finding solutions when creating larger fleet size formations, indicating savings surpassing 10%.